Distributive Property Math Definition Simple

The distributive property states that for real numbers a a b b and c c two conditions are always true.

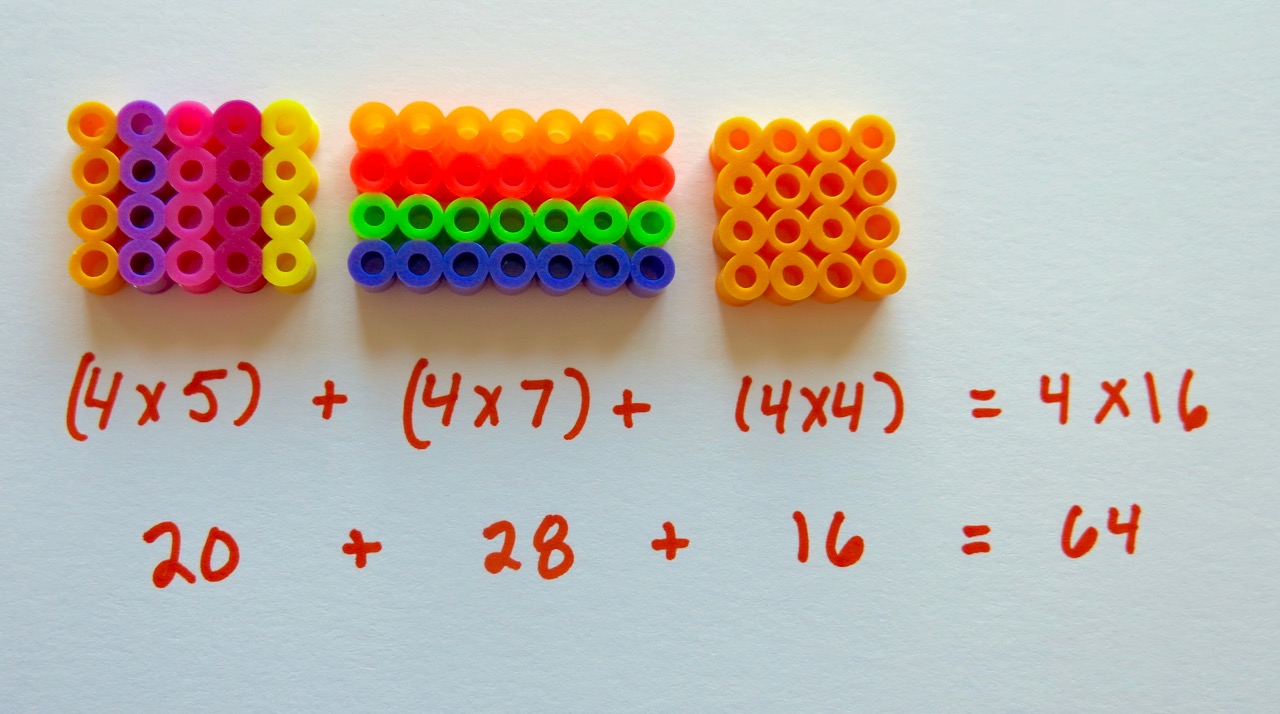
Distributive property math definition simple. In the end the best way to learn about the distributive property is to apply the concept to actual examples. And multiplication and subtraction. When we distribute something we are dividing it into parts. In general it refers to the distributive property of multiplication over addition or subtraction.

The distributive property is easy to remember if you recall that multiplication distributes over addition. To distribute means to divide something or give a share or part of something. This property states that two or more terms in addition or subtraction with a number are equal to the addition or subtraction of the product of each of the terms with that number. The distributive property is one of the most frequently used properties in basic mathematics.

Any time they refer in a problem to using the distributive property they want you to take something through the parentheses or factor something out. This is the currently selected item. A b c ab ac a b c a b a c. The distributive property is a property of multiplication used in addition and subtraction.

However if you are interested in a straightforward definition of distributive property there are a couple of simple things you can keep in mind. 3 2 4 3 2 3 4 so the 3 can be distributed across the 2 4 into 3 times 2 and 3 times 4. Any time a computation depends on multiplying through a parentheses or factoring something out they want. A b c ab ac a b c a b a c.

Formally they write this property as a b c ab ac. Distributive property is one of the fundamental properties of numbers and basic operations of mathematics. Distributive property connects three basic mathematic operations in two pairings. Basically this property gives you the ability to multiply sums by multiplying each component separately before setting about the task of adding your figures.

In general this term refers to the distributive property of multiplication which states that the. Factor with the distributive property no variables distributive property review. Distributive property over addition. The distributive property is one of the most frequently used properties in math.

This property refers to the distribution of multiplication over addition or subtraction. In numbers this means for example that 2 3 4 2 3 2 4. The distributive property lets you multiply a sum by multiplying each addend separately and then add the products. According to the distributive property multiplying the sum of two or more addends by a number will give the same result as multiplying each addend individually by the number and then adding the products together.

Math pre algebra arithmetic properties distributive property. Distributive property of multiplication. Hence it is most popularly known as the distributive property of multiplication over addition or subtraction. The distributive law says that multiplying a number by a group of numbers added together is the same as doing each multiplication separately.