Important Taylor Series Math

For most common functions the function and the sum of its taylor series are equal near this point. If the infinite series obtained is called taylor series for about. 1 the taylor series for y f x at x 0 is the power series.

octahedron surface area math apothem length math puzzle fun math 15 fraction math math square puzzle solver matthew 6 31 33 niv units of weight measure math ml in 1 liter math

Deriving Euler S Constant Using The Taylor Series Physics And Mathematics Studying Math Formulas

Https Files Vipulnaik Com Math 153 Sequence Taylorseries Pdf

Finding A Maclaurin Series Expansion Another Example 1 Youtube

Geometric Series

Maclaurin Series For Arctan X Youtube

Where Do Taylor Series Come From And Why We Learn About Them

Maclaurin Series To Evaluate A Limit Kristakingmath Youtube

Https Users Math Msu Edu Magyarp Math133 11 10 Taylor Series Pdf

The nth order maclaurin polynomial for y f x is just the nth order taylor polynomial for y f x at x 0 0 and so it is p n x xn n 0 f n 0 n.

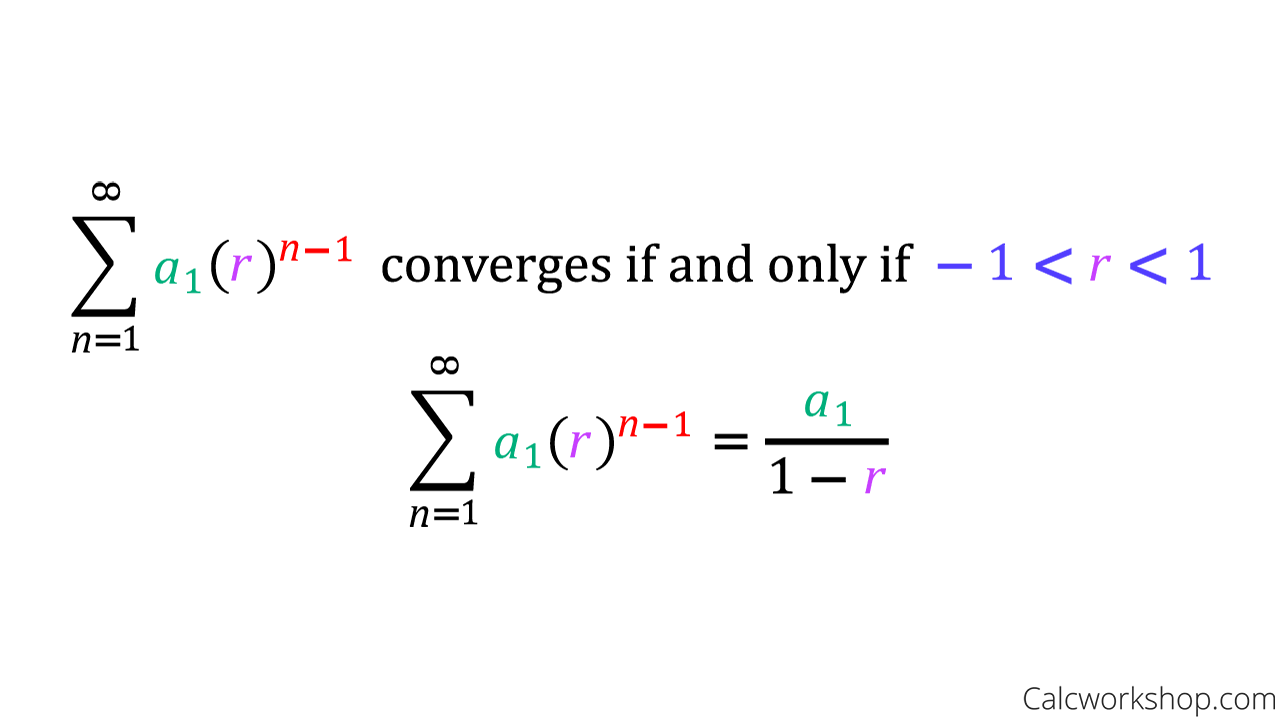
Important taylor series math. If the taylor series of a function f at x 0 converges to the values of f in a neighborhood of x 0 then f is real analytic in a neighborhood of x 0. In figure 3 3 we plot the four first terms of the series as a function of x for different times. If the series is often called a maclaurin series. X x 0 2 f n x 0 n.

N is the nth taylor coe cient of y f x about x 0. Here is the taylor series for this one. Its radius of convergence is rt for all t 0 1 and it is singular at t 1. A taylor series is a polynomial of infinite degrees that can be used to represent all sorts of functions particularly functions that aren t polynomials.

Taylor series represents the accumulation of several calculus topics and i would name it as one of the most significant results in calculus just behind both fundamental theorems and the mean value theorem. This result holds if has continuous derivatives of order at last. X 3 n f 3 f 3 x 3 f 3 2. X 3 3 0 57 33 x 3 x 3 2 x 3 3.

The taylor series for ex ex 1 x x2 2. The taylor series in x of f x t 1 t x for t 0 1 is. Taylor series a taylor series is an expansion of some function into an infinite sum of terms where each term has a larger exponent like x x 2 x 3 etc. P 1 x f x 0 f0 x 0 x x 0 f00 x 0 2.

This will always happen when we are finding the taylor series of a polynomial. σ r 0a nx n where a n log 1 t n n. If zero is the point where the derivatives are considered a taylor series is also called a maclaurin series after colin maclaurin who made extensive use of this special c. In mathematics the taylor series of a function is an infinite sum of terms that are expressed in terms of the function s derivatives at a single point.

Taylor series can be used to prove a multitude of identities including the famous euler s formula. Taylor s series are named after brook taylor who introduced them in 1715. X 3 10 x 2 6 n 0 f n 3 n. It can be assembled in many creative ways to help us solve problems through the normal operations of function addition multiplication and composition.

X x 0 n. Definition of taylor series. X 3 2 f 3 3.