Not Mutually Exclusive Definition Math

P a and b 0 the probability of a and b together equals 0 impossible. In logic and probability theory two events or propositions are mutually exclusive or disjoint if they cannot both occur at the same time. In the venn diagram above the probabilities of events a and b are represented by two disjoint sets i e they have no elements in common.

rounded definition math 100 times 2 math logic questions in maths angle of math additive identity property example math square m to square cm math simpson calculator math solution math definition example

Statistics Teaching Resources Ks3 And Ks4 Worksheets Learning Mathematics Probability Math

Non Mutually Exclusive Event Probability Example Youtube

Http Mrpaynemath Weebly Com Uploads 3 8 9 38994693 Math3201ch3 4notes Workings Pdf

Probability Of Mutually Exclusive Events With Venn Diagrams Youtube

Mutually Exclusive In Statistics Definition Formula Examples Video Lesson Transcript Study Com

Reinforce The Concept Of Probability With This Sorting Activity Students Will Sort Cards As Being Impossi Activities

Ap Chapter 5 Tps4e Statistics Math Probability

3 2 Independent And Mutually Exclusive Events Elementary Statistical Methods

Thus they must have at least one common point between them.

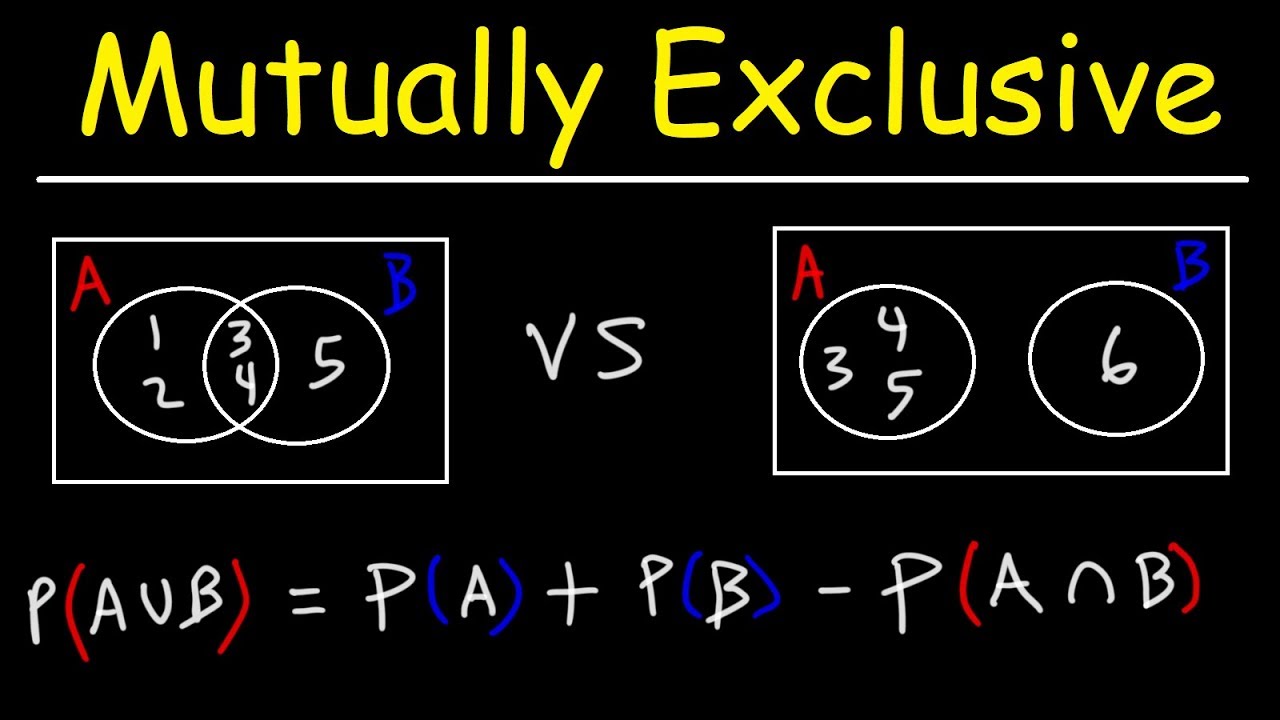
Not mutually exclusive definition math. Two events are mutually exclusive if they cannot occur at the same time i e they have no outcomes in common. These are not mutually exclusive because some outcomes are both odd and perfect squares 1 and 9. If the two events a and b are not mutually exclusive events then a b ϕ. In the coin tossing example both outcomes are in theory collectively exhaustive which means that at least one of the outcomes must happen so these two possibilities together exhaust all the possibilities.

However not all mutually excl. P a or b p a p b p a and b dependent and independent events. Well mutually exclusive means that if you have a and b then a and b can never be true at the same time. Events that can t happen at the same time.

Two events are called not mutually exclusive if they have at least one outcome in common. But kings and hearts are not mutually exclusive because you can have a king of hearts. When two events call them a and b are mutually exclusive it is impossible for them to happen together. If the events a and b are not mutually exclusive the probability of getting a or b is given as.

Let p s be the probability of a perfect square. Let p o be the probability of an odd number. P o or s p o p s p o and s p o. Kings and aces are mutually exclusive.

Not mutually exclusive is the reverse of this it means that a and b could be true at the same time. A clear example is the set of outcomes of a single coin toss which can result in either heads or tails but not both. Two events are non mutually exclusive if they have one or more outcomes in common. A card can t be an ace and a king at the same time.

Similarly a b and c are not mutually exclusive events if a b c ϕ.