Planar Graphs In Discrete Mathematics

Draw if possible two different planar graphs with the same number of vertices edges and faces.

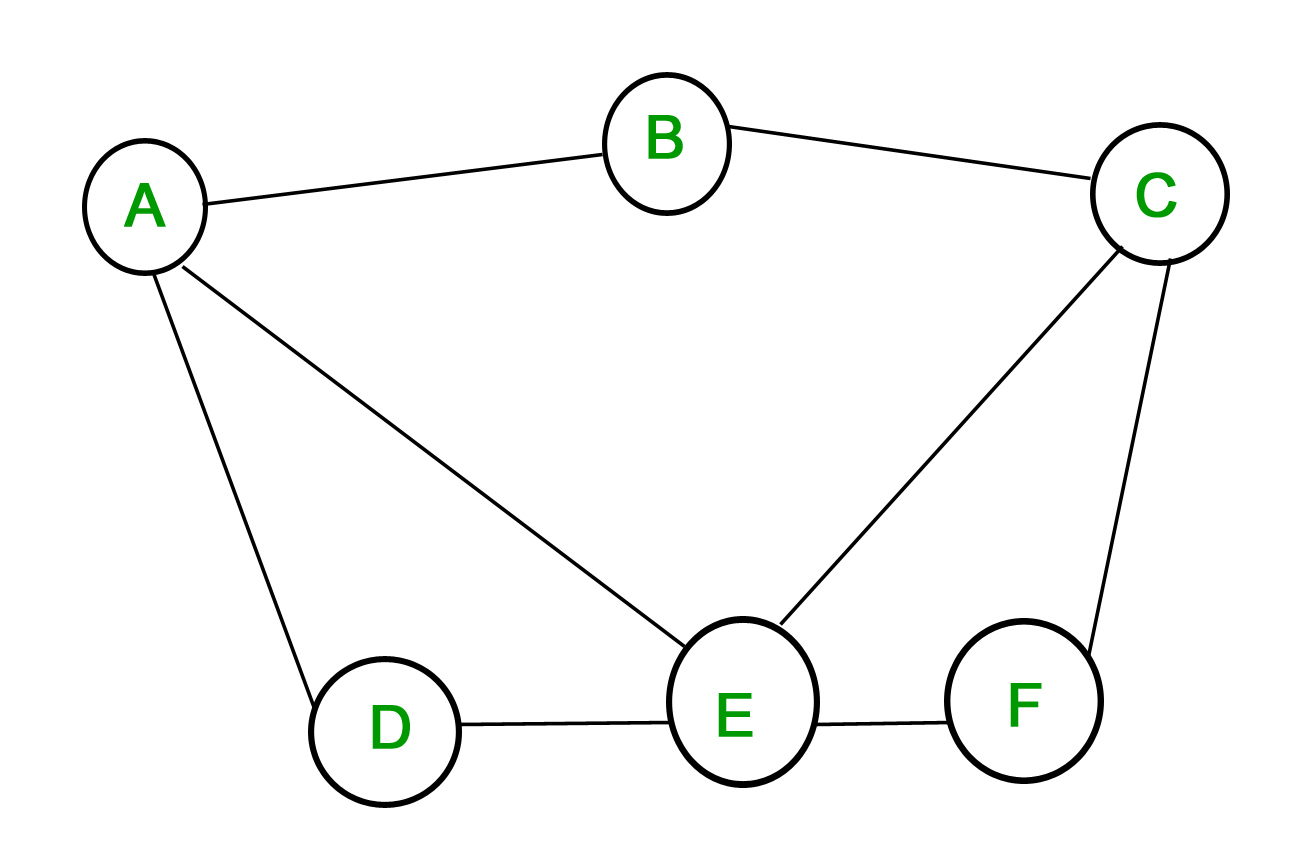
Planar graphs in discrete mathematics. When a planar graph is drawn in this way it divides the plane into regions called faces. When a connected graph can be drawn without any edges crossing it is called planar. In mathematics and more specifically in graph theory a graph is a structure amounting to a set of objects in which some pairs of the objects are in some sense related. Important note a graph may be planar even if it is drawn with crossings because it may be possible to draw it in a different way without crossings.

Draw if possible two different planar graphs with the same number of vertices edges and faces. A graph with six vertices and seven edges. Planarity a graph is said to be planar if it can be drawn on a plane without any edges crossing. We know that for a connected planar graph 3v e 6 hence for k 4 we have 3x4 6 6 which satisfies the property 3.

A complete bipartite graph k mn is planar if and only if m. Such a drawing is called a planar representation of the graph. The complete graph k 4 contains 4 vertices and 6 edges. A complete graph k n is a planar if and only if n.

Thus k 4 is a planar graph. Prove that complete graph k 4 is planar.