Z Score Of 95 Math

And so that is a z score of 0 53.

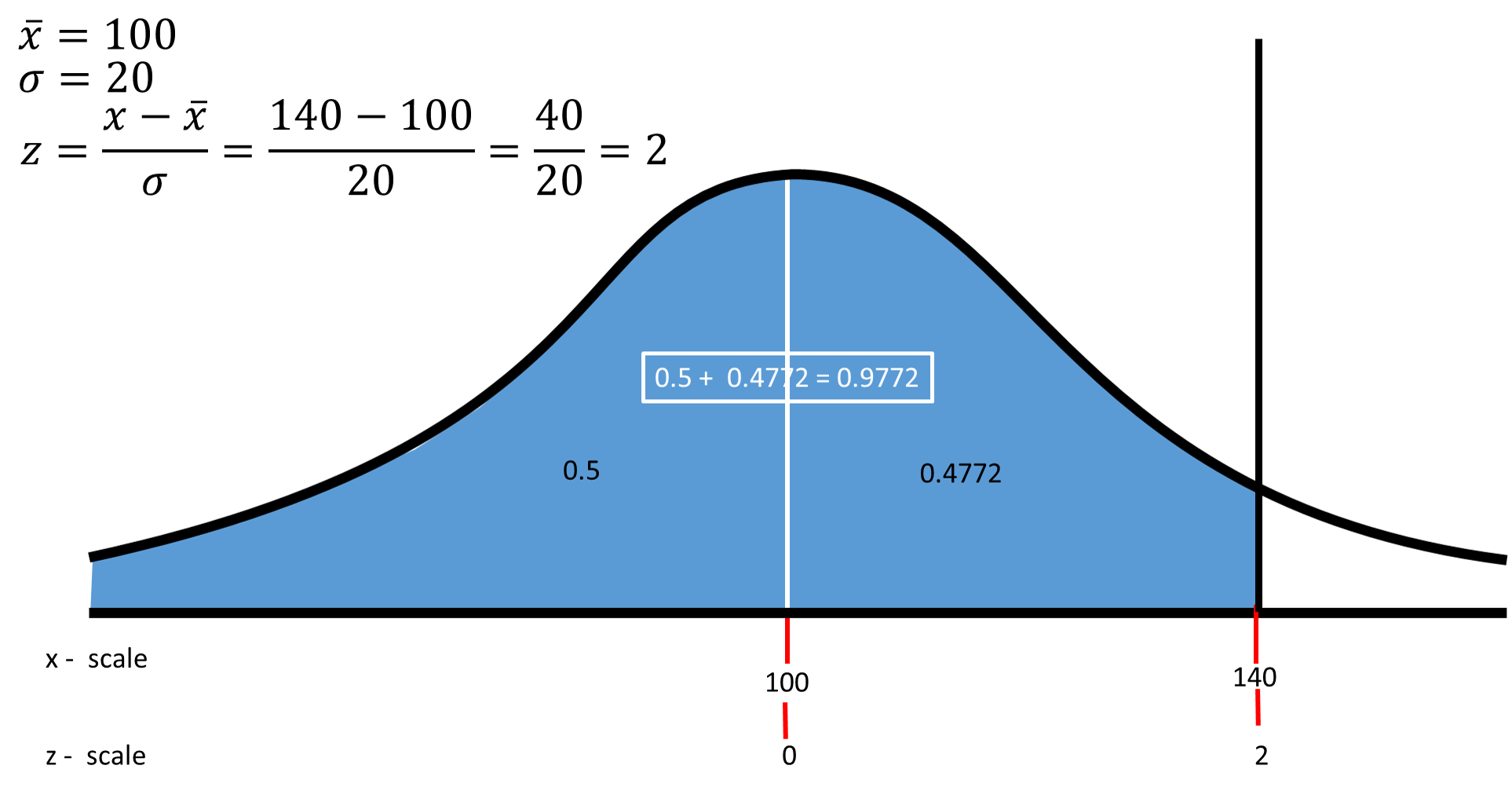
Z score of 95 math. To avoid all these extra steps and headaches the z table has already done this conversion for you. Since α 0 95 the area under the curve is 1 α 1 0 95 0 05 our critical z value is 1 6449 in microsoft excel or google sheets you write this function as normsinv 0 05 calculate left tailed value. It s also the number with 95 lying between two z values z and z. It is the area in percentage terms that is to the left of that z score.

Assuming a normal distribution of scores 95 of her students would score between what two values. Our critical z value. So it definitely crosses the threshold. 0 52 is too little.

Given α 0 95 calculate the right tailed and left tailed critical value for z calculate right tailed value. This is going to be 21 divided by 10. Z x bar x sigma 1 6449 x 80 6 9 8697 x 80 x 89 8697 so a score of x 90 will be above 95 of the scores. Let s write that down.

So on the lsat this is what. Mathematically for a given z score z we compute p. The score that corresponds to this z score can be found as follows. You could view this as a z score.

0 53 right over there and we just now have to figure out what value gives us a z score of 0 53. That s the z value with 97 5 area below it. The z score for her biology test is 5 65 60 10 representing 5 standard deviations above the mean and a percentile of 69. And that s exactly how we define the percentile associated to a z score.

For the statistics test we need to know that the mean was 37 with a standard deviation of 5. To get the total area below this z value take the 95 between z and z plus the 2 5 below z and you get 97 5. Also a z score represents a specific location in the distribution so that there is a certain area that is to the left of that z score. So we need a z score of 0 53.

So this is 2 1 standard deviations deviations above the mean above the mean. 58 90 professor ivy s students have a mean grade of 69 5 and a standard deviation of 6 5. Values above the mean have positive z scores while values below the mean have. Both data sets model a normal distribution which allows us to calculate z scores.